磁面与磁场的表示

环对称坐标下的磁场

磁失势的存在性与磁场的规范不变性

Maxwell方程组中的Ampère环路定律断言磁场无旋，

\begin{equation}\label{eq:磁场无旋}
\div{\bm{B}}=0.
\end{equation}

由此可以证明，磁场必可表为一矢量场之旋度，

\begin{equation}\label{eq:磁场可表为磁矢势之旋度}
\bm{B}=\curl{\bm{A}}.
\end{equation}

证明如下，定义矢量场 $\mathbfscr{A}$，

\begin{equation}\label{eq:磁矢势之表示}
\mathbfscr{A}\qty(\bm{r})\equiv\int_{0}^{1}\dd\lambda\bm{B}\qty(\lambda\bm{r})\crossproduct\qty(\lambda\bm{r}),
\end{equation}

则直接计算 $\mathbfscr{A}$ 的旋度即可知，

\begin{equation}\label{eq:磁矢势之旋度计算}
\begin{aligned}
\curl{\mathbfscr{A}\qty(\bm{r})}={}&\int_{0}^{1}\dd\lambda\curl\qty[\bm{B}\qty(\lambda\bm{r})\crossproduct\qty(\lambda\bm{r})]
\\
={}&\int_{0}^{1}\dd\lambda\qty{\qty[\qty(\lambda\bm{r})\dotproduct\grad]\bm{B}\qty(\lambda\bm{r})-\qty(\lambda\bm{r})\div{\bm{B}\qty(\lambda\bm{r})}+\bm{B}\qty(\lambda\bm{r})\div{\qty(\lambda\bm{r})}-\qty[\bm{B}\qty(\lambda\bm{r})\dotproduct\grad]\qty(\lambda\bm{r})}
\\
={}&\int_{0}^{1}\dd\lambda\qty{\qty[\qty(\lambda\bm{r})\dotproduct\grad]\bm{B}\qty(\lambda\bm{r})-\qty(\lambda^2\bm{r})\grad_{\lambda\bm{r}}\dotproduct\bm{B}\qty(\lambda\bm{r})+3\lambda\bm{B}\qty(\lambda\bm{r})-\lambda\bm{B}\qty(\lambda\bm{r})}
\\
={}&\int_{0}^{1}\dd\lambda\qty{\qty[\qty(\lambda\bm{r})\dotproduct\grad]\bm{B}\qty(\lambda\bm{r})-\underbrace{0}_{\text{磁场之 Gauss 定理}}+2\lambda\bm{B}\qty(\lambda\bm{r})}
\\
={}&\int_{0}^{1}\dd\lambda\qty[\lambda^2\dv{\bm{B}\qty(\lambda\bm{r})}{\lambda}+\dv{\lambda^2}{\lambda}\bm{B}\qty(\lambda\bm{r})]
\\
={}&\int_{0}^{1}\dd\lambda\dv{}{\lambda}\qty[\lambda^2\bm{B}\qty(\lambda\bm{r})]
\\
={}&\eval{\qty[\lambda^2\bm{B}\qty(\lambda\bm{r})]}_{\lambda=0}^{\lambda=1}
\\
={}&\bm{B}\qty(\bm{r}).
\end{aligned}
\end{equation}

因而 $\bm{B}$ 可以表为式 \eqref{eq:磁矢势之表示} 的旋度。将 $\mathbfscr{A}$ 作为式 \eqref{eq:磁场可表为磁矢势之旋度} 中的 $\bm{A}$，矢量 $\bm{A}$ 称为磁矢势。磁矢势的表达式并非唯一，可以相差一个标量场的梯度项。即，在规范变换

\begin{equation}\label{eq:磁矢势之规范变换}
\bm{A}\to\bm{A}+\grad{f},\forall f:\mathbb{R}^3\to\mathbb{R}
\end{equation}

下，磁场 $\bm{B}$ 不变，因为标量场的梯度为无旋场，

\begin{equation}\label{eq:标梯无旋}
\curl{\grad{f}}=0.
\end{equation}

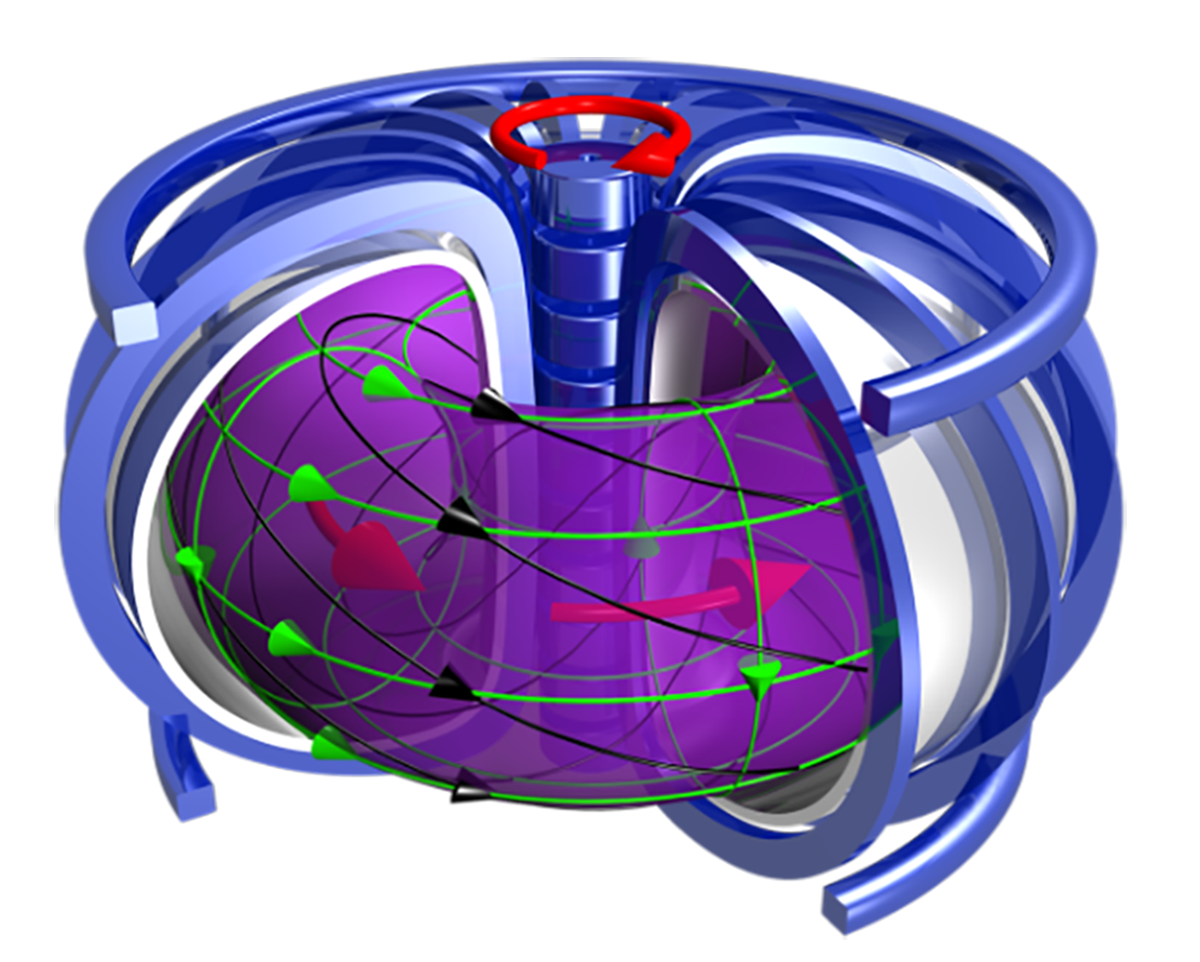
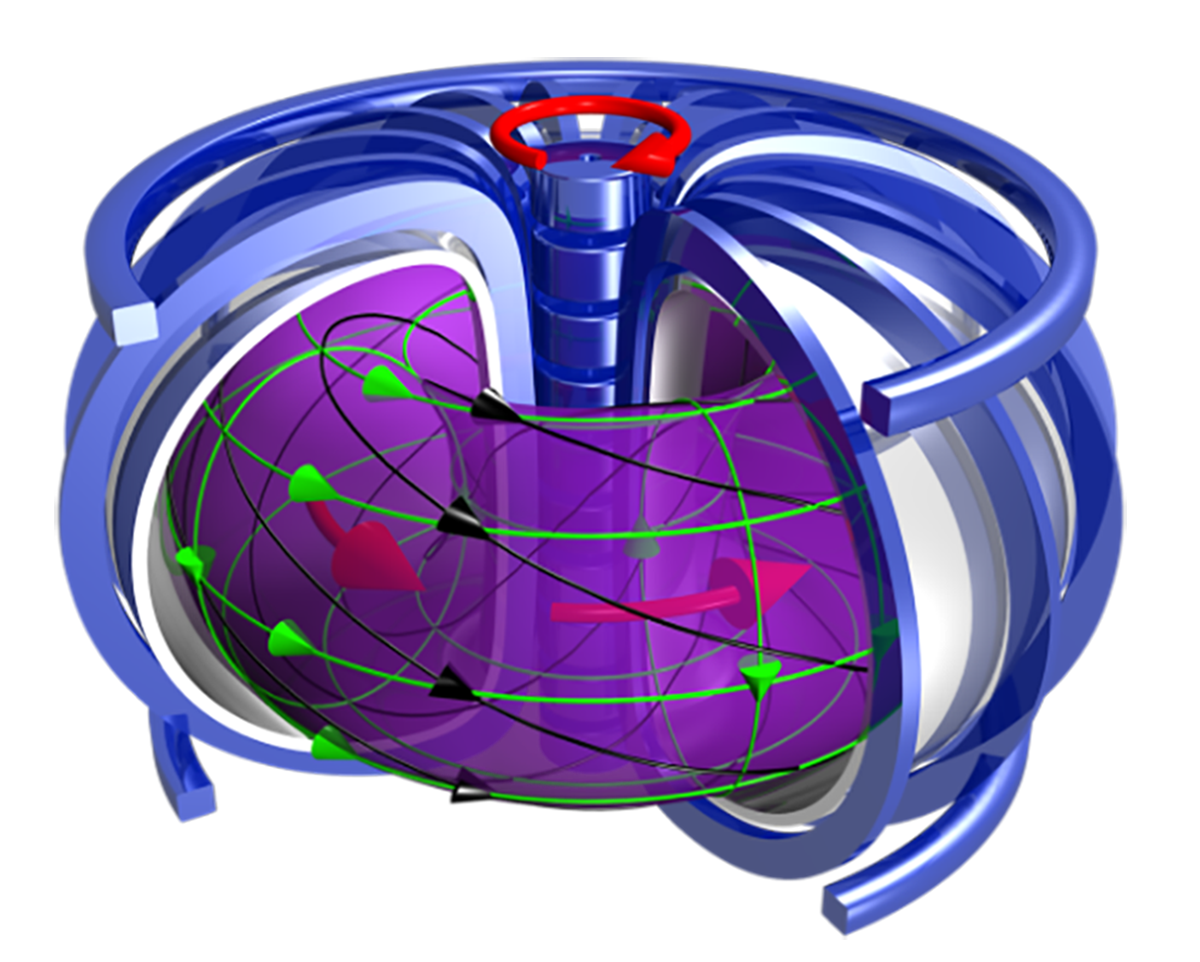
柱坐标下的 Tokamak 磁场

Tokamak 由一大环与一小环合并而成，具有环向（大环方向）与极向（小环方向）的周期性。

以 Tokamak 的大环平面为 $R-\phi$ 平面建立柱坐标系，则装置稳态运行时，可认为 Tokamak 中的等离子体具有环向对称性，即

\begin{equation}\label{eq:环向对称性}
\pdv{\mathcal{O}}{\phi}=0,\forall\mathcal{O}:\mathbb{R}^3\to\mathbb{C}.
\end{equation}

式 \eqref{eq:环向对称性} 的意义是，微分算子 $\pdv{}{\phi}$ 作用于任意“坐标系无关”的实或复标量场的结果均为 $0$。

将磁矢势之旋度 $\curl{\bm{A}}$ 以柱坐标系 $\qty(R,\phi,Z)$ 的单位基矢 $\qty(\bm{e}_R,\bm{e}_\phi,\bm{e}_Z)$ 为基展开，

\begin{equation}\label{eq:在柱坐标系基矢中展开旋度算子}
\curl{\bm{A}}=\bm{e}_R\qty(\frac{1}{R}\pdv{A_Z}{\phi}-\pdv{A_\phi}{Z})+\bm{e}_\phi\qty(\pdv{A_R}{Z}-\pdv{A_Z}{R})+\frac{\bm{e}_Z}{R}\qty[\pdv{\qty(RA_\phi)}{R}-\pdv{A_R}{\phi}],
\end{equation}

由式 \eqref{eq:环向对称性} 与式 \eqref{eq:在柱坐标系基矢中展开旋度算子} 可得

\begin{equation}\label{eq:考虑环向对称性后磁矢势之旋度}
\curl{\bm{A}}=-\bm{e}_R\pdv{A_\phi}{Z}+\bm{e}_\phi\qty(\pdv{A_R}{Z}-\pdv{A_Z}{R})+\frac{\bm{e}_Z}{R}\pdv{\qty(RA_\phi)}{R},
\end{equation}

由此可知，当系统具有环向对称性时，磁场的 $R$、$Z$ 分量仅由磁矢势的 $\phi$ 分量所决定。因此可以定义一个量，

\begin{equation}\label{eq:psi之定义}
\psi\equiv RA_\phi.
\end{equation}

此外，为方便起见，另外定义一个量，

\begin{equation}\label{eq:F之定义}
F\equiv R\qty(\pdv{A_R}{Z}-\pdv{A_Z}{R}).
\end{equation}

若将磁场分解为环向分量（又称为纵向分量）$\bm{B}_\mathrm{t}\equiv B_\phi\bm{e}_\phi$ 与极向分量（又称为角向分量）$\bm{B}_\mathrm{p}\equiv B_R\bm{e}_R+B_Z\bm{e}_Z$，则由式 \eqref{eq:磁场可表为磁矢势之旋度}，式 \eqref{eq:考虑环向对称性后磁矢势之旋度}，式 \eqref{eq:psi之定义}，式 \eqref{eq:F之定义} 可知，

\begin{equation}\label{eq:磁场之极向分量与环向分量}
\begin{cases}
\bm{B}_\mathrm{t}=\frac{F}{R}\bm{e}_\phi=F\grad{\phi},\\
\bm{B}_\mathrm{p}=-\frac{\bm{e}_R}{R}\pdv{\psi}{Z}+\frac{\bm{e}_Z}{R}\pdv{\psi}{R}=\bm{e}_Z\crossproduct\frac{\bm{e}_\phi}{R}\pdv{\psi}{Z}+\bm{e_R}\crossproduct\frac{e_\phi}{R}\pdv{\psi}{R}=\grad\psi\crossproduct\grad{\phi}.
\end{cases}
\end{equation}

因而总磁场可表为

\begin{equation}\label{eq:磁场用磁面表示}
\bm{B}=\grad{\psi}\crossproduct\grad{\phi}+F\grad{\phi}.
\end{equation}

式 \eqref{eq:F之定义} 所定义的 $F$ 十分形象，即磁场之环向分量 $B_\mathrm{t}$ 乘大半径 $R$。而式 \eqref{eq:psi之定义} 所定义的 $\psi$ 代表什么？为阐明其物理意义，可以计算磁场 $\bm{B}$ 在单位 $\phi$ 内的极向磁通微元，

\begin{equation}\label{eq:磁场之极向磁通}
\begin{aligned}
\dd{\mit{\Psi}}_\mathrm{p}={}&\dd{S}\hat{n}\dotproduct\bm{B}
\\
={}&R\dd{r}\Delta\phi\hat{n}\dotproduct\bm{B}
\\
={}&R\dd{r}\hat{n}\dotproduct\bm{B}
\\
={}&R\dd{r}\qty(-\sin\theta\bm{e}_R+\cos\theta\bm{e}_Z)\dotproduct\bm{B}
\\
={}&R\qty(-\dd{Z}\bm{e}_R+\dd{R}\bm{e}_Z)\dotproduct\bm{B}
\\
&\!\!\!\!\!\!\!\!\xlongequal{\text{代入式 \eqref{eq:考虑环向对称性后磁矢势之旋度} 和式 \eqref{eq:psi之定义}}}\qty(\pdv{\psi}{Z}\dd{Z}+\pdv{\psi}{R}\dd{R})
\\
={}&\qty(\pdv{\psi}{Z}\dd{Z}+\pdv{\psi}{R}\dd{R}+\underbrace{\pdv{\psi}{\phi}\dd{\phi}}_{=0})
\\
={}&\dd{\psi}.
\end{aligned}
\end{equation}

其中，极向面元 $\dd S$ 及其单位法向量 $\hat{n}$ 的示意如图 图 2 所示。

由式 \eqref{eq:磁场之极向磁通} 可知，$\psi$ 与单位 $\phi$ 内之极向磁通 ${\mit{\Psi}}_\mathrm{p}$ 最多相差一常数。不妨将此常数取为 $0$，故而 $\psi$ 之物理意义即为单位 $\phi$ 内之极向磁通。

磁面与磁面函数

磁场线与磁面

磁场线即为磁场 $\bm{B}$ 的积分曲线，线上的点 $\bm{r}$ 满足

\begin{equation}\label{eq:磁场之积分曲线}
\dv{\bm{r}}{\lambda}=\bm{B}\qty(\bm{r}),
\end{equation}

其中 $\lambda$ 为一任选参数，仅用于确定磁场线上点之位置，无需具有实际物理意义。

若空间中存在一个曲面，使有一条磁场线完全位于此曲面内，则称其为一磁面。磁面之方程并非唯一，仅需满足 $\bm{B}\qty(\bm{r})\in T_{\bm{r}}\mathcal{M}$ 或 $\hat{n}_\mathcal{M}\qty(\bm{r})\dotproduct\bm{B}\qty(\bm{r})=0$，其中 $\mathcal{M}$ 为磁面，$T_{\bm{r}}\mathcal{M}$ 为磁面在 $\bm{r}$ 处的切空间，$\hat{n}_\mathcal{M}\qty(\bm{r})$ 为磁面上 $\bm{r}$ 处的（单位）法向量。

作为磁面之磁通函数等值面

由于环向对称性，式 \eqref{eq:psi之定义} 所定义的 $\psi$ 仅为 $R$, $Z$ 的函数，而与 $\phi$ 无关。即 $\psi=\psi\qty(R,Z)$。$\psi$ 的等值面可作为磁面。证明如下，

\begin{equation}\label{eq:磁通函数等值面可作为磁面}
\begin{aligned}
\grad\psi\dotproduct\bm{B}={}&\grad\psi\dotproduct\qty(\grad\psi\crossproduct\grad\phi+F\grad\phi)
\\
={}&F\grad\psi\dotproduct\grad\phi
\\
={}&F\qty(\bm{e}_R\pdv{\psi}{R}+\bm{e}_Z\pdv{\psi}{Z})\dotproduct\frac{\bm{e}_\phi}{R}
\\
={}&0.
\end{aligned}
\end{equation}

而 $\grad\psi$ 为 $\psi$ 等值面的法向量，因而 $\hat{n}_\psi\propto\grad\psi$，故 $\hat{n}_\psi\dotproduct\bm{B}=0$，$\psi$ 可作为磁面。